Open In Colab

线性回归

先从一个图例来认识线性回归

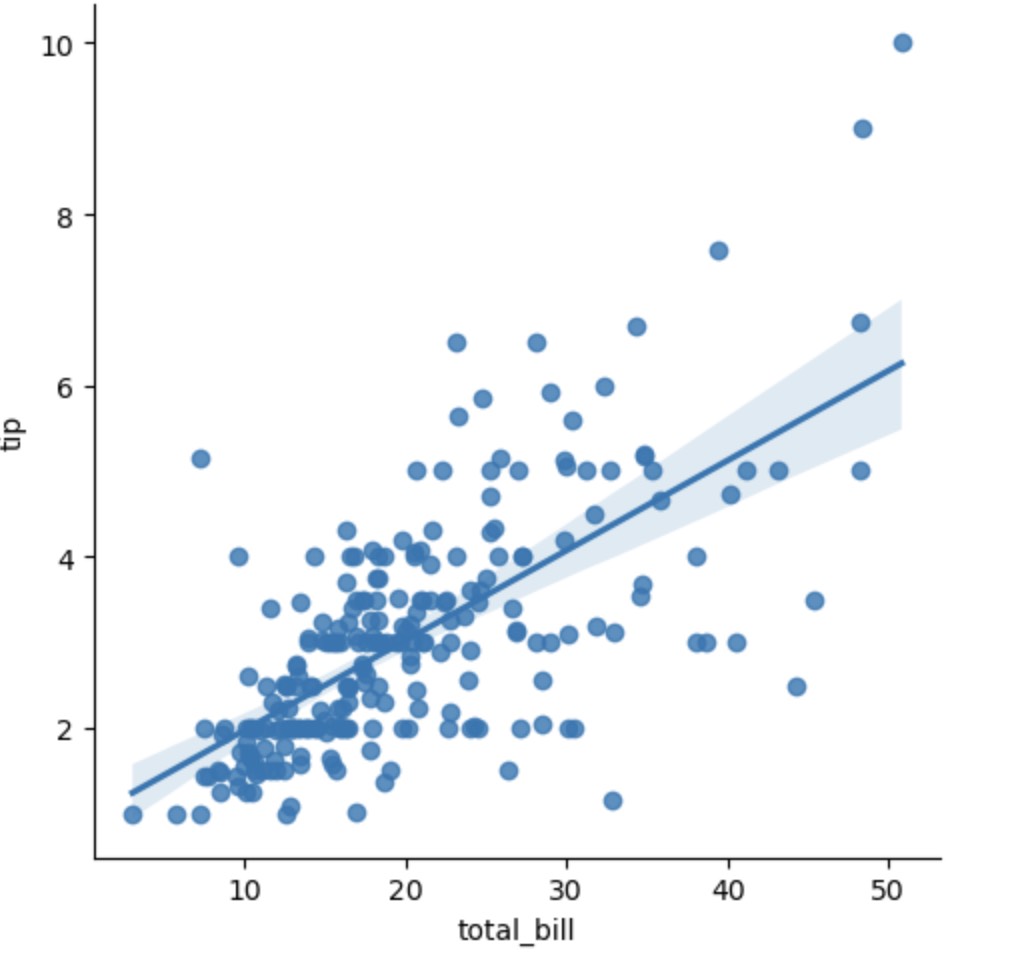
lmplot

下面用这个公式来实现线性回归 样例数据集 $$\hat{y_i} = \bar{y} + r \frac{SD(y)}{SD(x)} (x_i - \bar{x})$$

  • x 为账单,y 为小费
  • r为相关系数
1
2
3
4
5
6

x_bar = np.mean(tips["total_bill"])
y_bar = np.mean(tips["tip"])
std_x = np.std(tips["total_bill"])
std_y = np.std(tips["tip"])
r = np.corrcoef(tips['total_bill'],tips['tip'])[0][1]
r

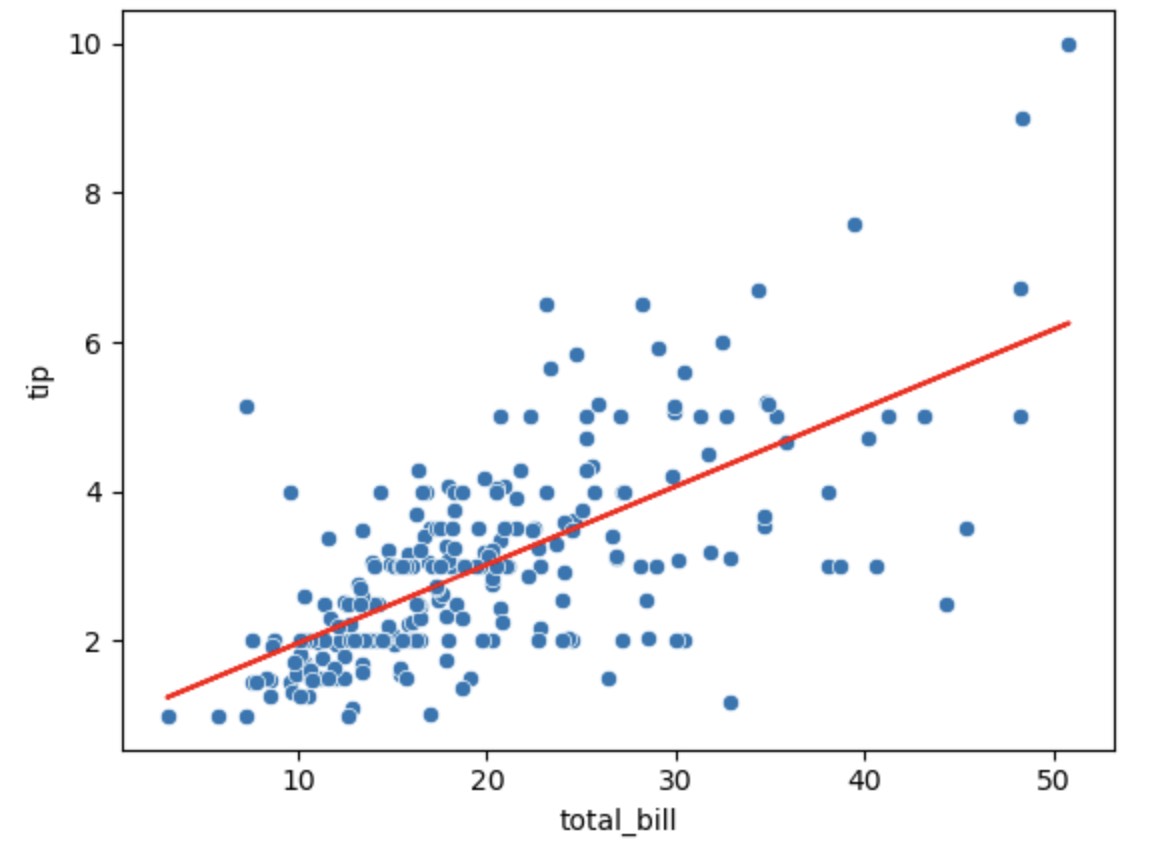
根据上述系数和截距来画图

1
2
3
4
5

regression = a_hat + b_hat * tips['total_bill']
sns.scatterplot(x="total_bill", y="tip", data=tips)
plt.plot(tips["total_bill"], regression, color="r")
plt.xlabel("total_bill")
plt.ylabel("tip");

lab07_2

使用Minimize

L2优化

$$R(a, b) = \frac{1}{n} \sum_{i = 1}^n(y_i - (a + b x_i))^2$$

1
2
3
4
5
6

def l2_tip_risk_list(theta):
    """Returns average l2 loss between regression line for intercept a
    and slope b"""
    a = theta[0]
    b = theta[1]
    return np.mean(np.power(tips['tip']-(a+b*tips['total_bill']),2))

多元线性回归

数据集

多元线性回归公式:

$$y_i = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + … + \theta_p x_p $$

1
2
3
4
5
6
7
8
9


desired_columns = ['horsepower','hp^2','model_year','acceleration']
model_many = LinearRegression()
model_many.fit(X=vehicle_data[desired_columns], y=vehicle_data["mpg"])
predicted_mpg_many = model_many.predict(
    vehicle_data[["horsepower", "hp^2", "model_year", "acceleration"]]
)
sns.scatterplot(x="horsepower", y="mpg", data=vehicle_data)
plt.plot(vehicle_data["horsepower"], predicted_mpg_many, color="r");