Lab06_WriteUp

模型, 统计, 损失函数

损失函数

损失函数是我们用来确定我们模型的最佳参数的。

损失函数是对一个模型能够预测预期结果的程度的一种衡量。换句话说，它衡量的是预测值与观察值的偏差。在这个实验室中，我们将实现平方损失和绝对损失函数。

下面公式里面$y$ 代表观察值，$\hat{y}$ 代表预测值

1. Squared Loss(平方损失) (也叫the $L_2$ 损失函数, 发音 “ell-two”):

$$\Large L(y, \hat{y}) = (y - \hat{y})^2$$

1. Absolute Loss(绝对损失) ( 也叫$L_1$ 损失函数, 发音"ell-one"):

$$\Large L\left(y, \hat{y} \right) = \left| y - \hat{y} \right|$$

我们使用如下的常量模型 $\hat{y} = \theta$ 做实验, 我们会用下面的两个函数 $(y - \theta)^2$ 和 $|y - \theta|$ 来代替上述提到的损失函数.

平方损失

$$\Large L\left(y, \theta \right) = \left( y - \theta \right)^2 $$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

def squared_loss(y_obs, theta):
    """
    Calculate the squared loss of the observed data and a summary statistic.

    Parameters
    ------------
    y_obs: an observed value
    theta : some constant representing a summary statistic

    Returns
    ------------
    The squared loss between the observation and the summary statistic.
    """
    return np.power(y_obs-theta,2)

图例:

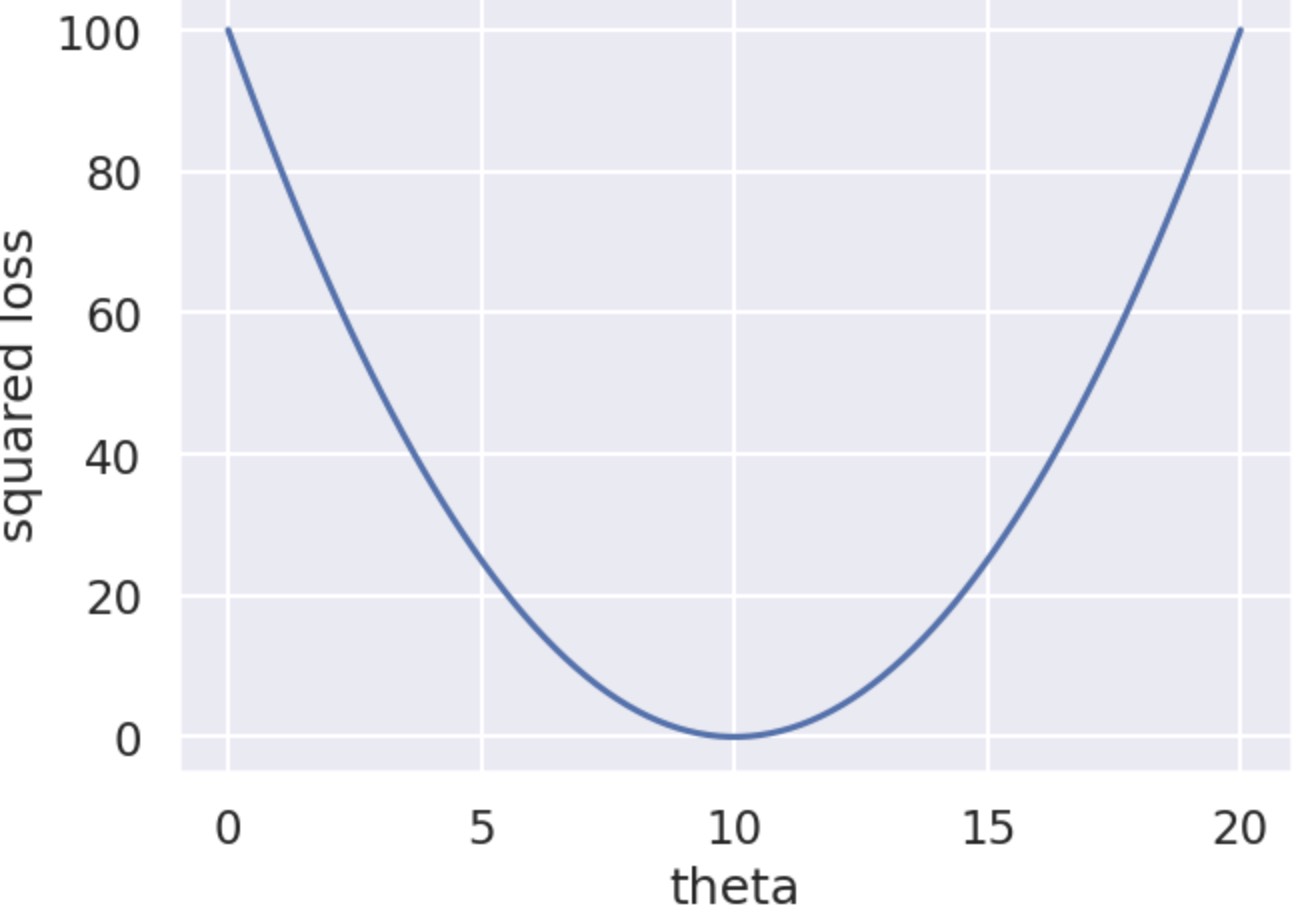
绝对损失

$$\Large L\left(y, \theta \right) = \left| y - \theta \right| $$

1
2

def abs_loss(theta, y_obs):
    return np.abs(y_obs-theta)

图例:

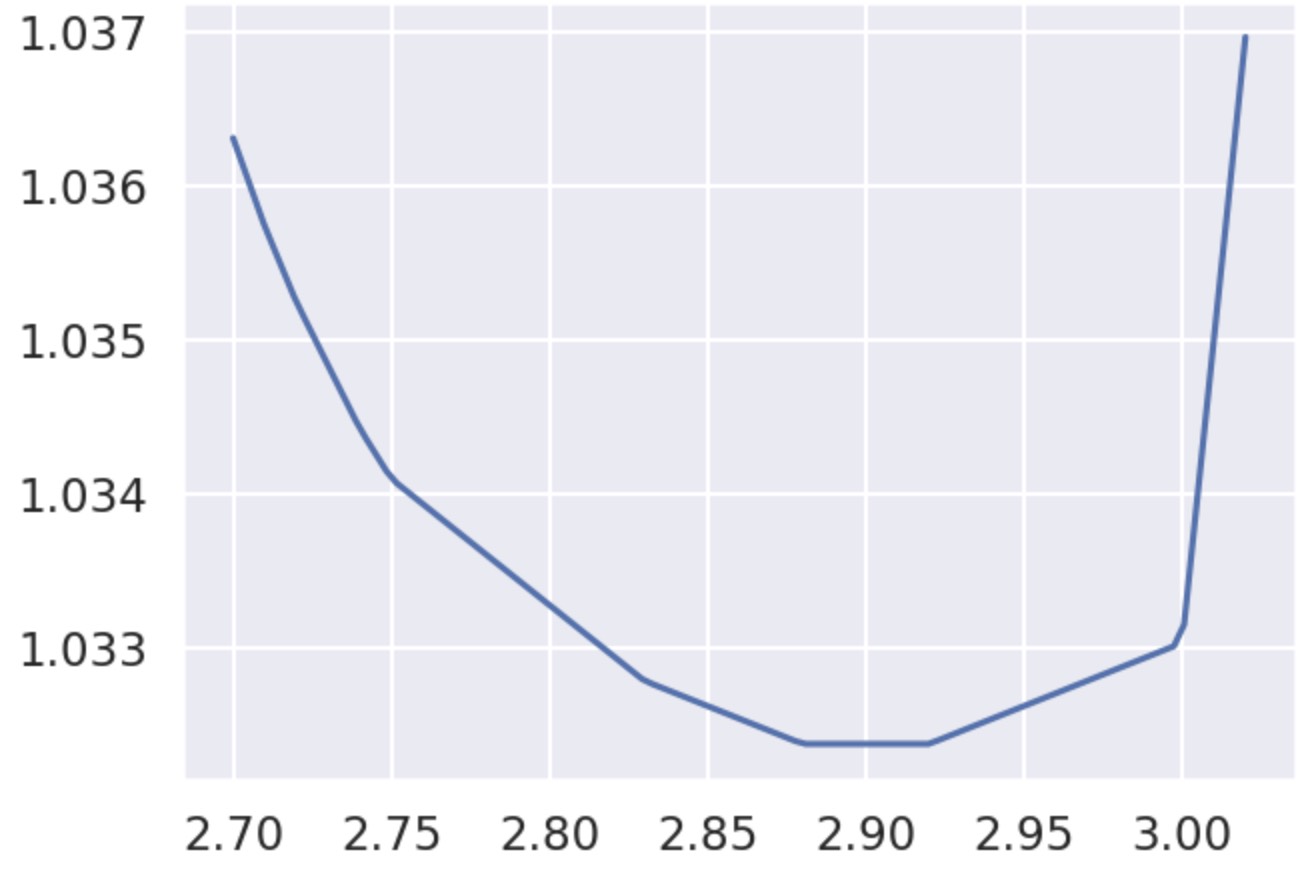
区别

MAE(平均绝对误差) 与MSE(均方误差)的几个区别

1. 最小化的$\theta$是不同的。
2. 当我们远离最小化$\theta$时，MAE的曲线呈线性增长，而不是呈二次增长。
3. MAE的曲线是线性的，而不是平滑的。斜率的每次变化都发生在我们数据集中的同一个$\theta$值