Day5
描述
下面给出一个输入样例,这个问题有点像汉诺塔问题
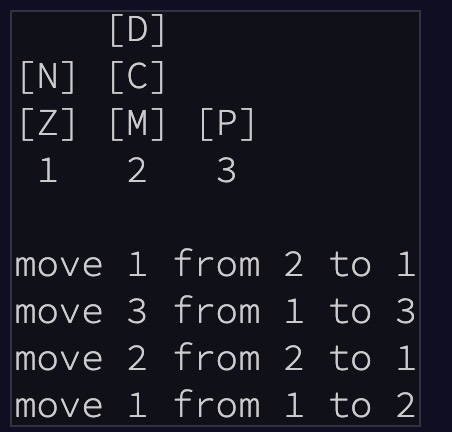
大意就是:
- 第一次从第二个栈里面移动 1 个元素到第一个栈里面
- 第二次从第一个栈移动 3 个元素到第三个栈里面
- 第三次移动 2 个元素从第二个栈到第一个里面
- 第四次移动第一个栈里的 1 个元素到第二个栈里面
最终结果展示:

因此第一部分最终的栈顶元素为CMZ
第二部分和第一部分的区别就是入栈的时不是按照出栈的顺序而是相反的
解法
这个问题主要处理在数据的处理上首先数据分为两部分
- 矩阵数据包括每个栈的元素
- 操作列表,需要用来解析出操作开始栈的下标和结束栈的下标,以及需要操作的次数
我的输入:

1
2
3
4
5
6
7
8
|
operations = [(i.split(' ')[1],i.split(' ')[3],i.split(' ')[5]) for i in d.split('\n')]
ans = []
for i in t.split('\n')[:8]:
temp = [ i[1+4*j] for j in range(9)]
ans.append(temp)
matrix = np.array(ans)
actual_data = [ list("".join(i[::-1]).replace(' ','')) for i in matrix.T.tolist()]
|

Part I
1
2
3
4
5
6
7
8
| def solution_day5_part1(operations, actual_data):
for i in operations:
cnt, start, end = i
m, n, p = int(cnt), int(start) - 1, int(end) - 1
for j in range(m):
pop1 = actual_data[n].pop()
actual_data[p].append(pop1)
return "".join([i[-1] for i in actual_data])
|
Part II
1
2
3
4
5
6
7
8
9
10
| def solution_day5_part2(operations, actual_data):
for i in operations:
cnt, start, end = i
m, n, p = int(cnt), int(start) - 1, int(end) - 1
for j in range(m):
pop1 = actual_data[n].pop()
actual_data[p].append(pop1)
l = len(actual_data[p]) - m
actual_data[p] = actual_data[p][:l] + actual_data[p][l:][::-1]
return "".join([i[-1] for i in actual_data])
|
总结
这个问题的直觉解法就是利用了栈的特性
主要问题是处理数据的输入
下面这段一行代码是用来处理输出的(来源于PythonDiscord)
1
2
3
4
5
6
7
8
9
10
11
12
| s = \
""" [C] [B] [H]
[W] [D] [J] [Q] [B]
[P] [F] [Z] [F] [B] [L]
[G] [Z] [N] [P] [J] [S] [V]
[Z] [C] [H] [Z] [G] [T] [Z] [C]
[V] [B] [M] [M] [C] [Q] [C] [G] [H]
[S] [V] [L] [D] [F] [F] [G] [L] [F]
[B] [J] [V] [L] [V] [G] [L] [N] [J]
1 2 3 4 5 6 7 8 9 """
print([''.join(x).strip() for x in zip(*(l[1::4] for l in s.splitlines()[-2::-1]))])
|



